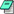jeffrey.kissel@LIGO.ORG - posted 18:08, Tuesday 14 February 2017 - last comment - 09:27, Monday 06 March 2017(34153)
All-of-O2 Trend (thus far) of PCALY RXPD vs. TXPD: How Early Jan. Clipping Effects on Time-Dependent Correction Factors and h(t)
J. Kissel, S. Kandhasamy As we begin to produce the systematic error budget for H1's response function, we're looking to figure out how to address the clipping of light going into H1 PCAL Y's RX PD that had been revealed in early January (see LHO aLOG 33108 and 33187). Because we got extremely lucky and took the 2017-01-03 reference measures at a time when the clipping -- which had been found to be slowly varying as a function of time -- had varied briefly back to nominal, this problem does not create any impact on the static, frequency-dependent part of the calibration pipeline. However, because the small, time-dependent correction factors are calculated using the H1 PCALY RXPD, these correction factors are systematically biased. Working through the math of T1500377, specifically Eqs. 9, 12, 15, and 16, one can see that while the cavity pole frequency estimate would not be impacted, the scalar correction factors are: If x_pcal' = eps x_pcal where eps is a real number (the number to convert the apparent displacement, x_pcal, into the real displacement, x_pcal'), then kappa_TST' = eps kappa_TST and kappa_PU' = (1 / A_0^PU) [A_total' - kappa_TST' A_0^TST] (A_total' = eps A_total, from Eq. 11) = (eps / A_0^PU) [A_total - kappa_TST A_0^TST] = eps kappa_PU and finally, S' = (1 / C_res) [ x_pcal' / d_err - D_0 (kappa_TST' A_0^TST + kappa_PU' A_0^PU)]^-1 S' = eps S such that kappa_C' = |S'|^2 / Re[S'] = (1 / eps) kappa_C which means that we can simply scale the entire response function with this time-dependent systematic error: R' = [1 / (kappa_C' C_0) ] + [kappa_PU' A_0^PU + kappa_TST' A_0^TST] = [eps / (kappa_C C_0)] + eps [kappa_PU A_0^PU + kappa_TST A_0^TST] R' = eps R I attach a 77 day minute trend of the ratio between RXPD and TXPD that's been obtained from data viewer***. I'm not yet advocating that time-series this be used as the representative systematic error, but I post it to be demonstrative. Stay tuned on how this data is encorporated into the uncertainty / error budget. *** Because it's data viewer, it spits out some dumb Julian calendar time vector. Just subtract off the first value, and you get a time vector in days since the start of the trend, which is Nov 30 2016 00:54:44 UTC. The data also lives in the CAL repo here: /ligo/svncommon/CalSVN/aligocalibration/trunk/Runs/O2/H1/Measurements/PCAL/ 2017-02-14_H1PCALY_RXPD_Trend.txt 2017-02-14_H1PCALY_TXPD_Trend.txt The script used to process this data and plot the figure is here: /ligo/svncommon/CalSVN/aligocalibration/trunk/Runs/O2/H1/Scripts/PCAL/ plot_h1pcaly_RXvsTXPD_trend_20170214.m
Non-image files attached to this report
Comments related to this report
J. Kissel, on behalf of S. Karki and C. Cahillane.
The data provided by Sudarshan via SLM tool that represents the PCAL clipping actually used by Craig in his systematic error budget for CBC analysis chunks 2 & 3 during O2 -- i.e. from Nov 30 2016 17:09:39 UTC to Jan 22 2017 04:36:04 (1164560996 to 1169094982) -- has been committed to the svn here:
${CalSVN}/aligocalibration/trunk/Runs/O2/H1/Results/PCAL/
O2_RxPD_TxPD_factor_dcsready.txt
I attach a .png of the data also committed to the same location.
Images attached to this comment
Non-image files attached to this comment