Stefan, TVo, TJ, Danny
Stefan has the idea of significantly reducing the amount of time it takes a test mass to reach a final lens by utilizing the ring heater step response and carefully designing an inverse filter to realize the inverse response. We tested the idea in a previous post using Comsol data and were able to get a time series of the ring heater settings necessary to achieve a "step lens". To test this with measured data I took a time series from H1:TCS-ITMY_HWS_PROBE_SPHERICAL_POWER after the ring heater settings had been changed by a reasonably large amount and attempted to perform the same procedure. The matlab zpk model of the system filter and inverse filter are attached figures. There are also comparison figures of the ring heater inputs and another figure their respective responses.
Testing the new ring heater time series:
With an initial lens around 3 microdiopters, the following figure shows convergence to a final lens of approximately -16 +/- 3 microdiopters within the first three hours but is about 1/2 the predicted lens. I might need to take another look at my model to see why this might be.
I cut the script the short because there will probably be commissioners coming in tomorrow so I am using this method (on workstation ZOTWS2) in attempts to restore the original ITMY lens by tomorrow morning (but will run till 9/31 00:00 PST to maintain the lens).
Could the same missing 50% explain why the preloading was off?
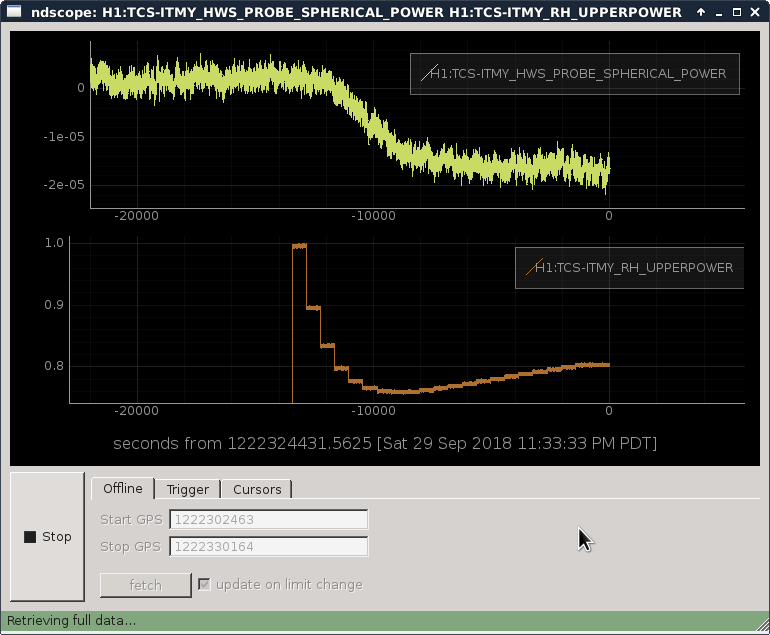
Sorry Daniel. This 50% was due to a couple of ridiculous mistakes on my part. The first mistake was that I assumed that the initial step response was caused by a ring heater step of 1 watt when in reality it was caused by a step of 3.13 watts (please see attached image for updated plant zpk model with new gain). The second, and most glaring mistake, was not thinking about the additive power from both of the upper and lower portions of the ring heaters so this left a factor of two missing in my model. I've attached time series of the measured data of the ring heater power compared to the time series from the updated model. I've attached a spherical power time series comparison as well. The final differential lens that the model suggests is 18.98 microdiopters.
In regards to pre-loading, I can update you on how these time series compare to the TCS simulation time series whose input parameters are used in the pre-loading estimates.
The model of the pre-loading estimates use the calibration in diopters/watt on the TCS simulation page.
Spherical power (udiopters) = [ 2*(-9E-6) + 0.9E-6] * P_RH = -17 udiopters for 1 Watt
The first coefficent in the equation is the substrate lens (the factor of 2 for double passing) and the second coefficient is the radius of curvature change.
Here is a comparison plot with the added TCS simulation time series. The simulation appears to be converging to a differential lens of 18 +/- 1 microdiopters.