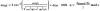Sheila, Daniel, Nutsinee
Last week we measured a set of sqz/asqz vs. CLF angle measurement. Using equation 2.71, 2.71, and 4.5 from Sheila's thesis and some adjustment to CLF angle read back we were able to make a reasonable fit to the measurement.
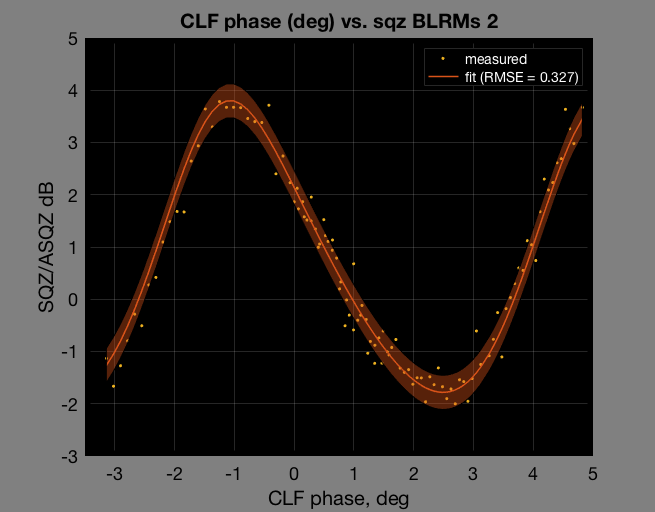
There are 5 variables, loss, phase noise, initial offset, CLF angle offset, and sqz angle offset. The uncertainty band is the rms error value between the fit and the measured data. To get the uncertainty on each parameter I tweaked each one to the point the rmse is increased by 10%, which at that point the fit looked very unlikely to be a good fit, giving us the upper bound of the uncertainty of each variable. Suggestion by David McManus.
Loss = 51.86% +/- 5%
Phase noise (rad) = 0.1577 +0.066/-0.1177
Initial offset (rad) CLF angle offset (rad) = 3.789 +/- 0.023
CLF angle offset (rad) Ellipse Axes ratio (r as Daniel described below) = 1.7252 +0.1693/-0.1327
SQZ angle offset (rad) = -1.0304 +0.0654/-0.0151
CLF angle offset is the discrepancy between the slide bar read back and the real angle offset. This was due to unequal side bands.
The relation between demodulation angle and squeezer angle can be written as
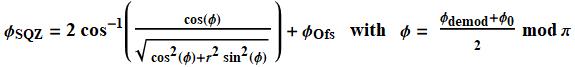
with:
ϕdemod : demodulation angle
ϕ0 : offset to the demodulation angle
ϕSQZ : squeeze angle
ϕOfs : offset to the squeeze angle
r : ratio between major and minor axes of the demodulation ellipse in the IQ plane
The ratio r is related to the non-linear gain of the CLF field.
The above fit uses ϕOfs as the squeeze angle offset and ϕ0/2 as the demodulation (CLF) offset.
If I were to tweak one parameter and let the function re-fit the rest of the parameters (as all of these variables are dependent of each other), using the same criteria as before (10% increase in RMSE) here's what I came up with in terms of uncertainty:
Loss (%) = 51.86 +14.64/-8.56
Phase noise (rad) = 0.1577 +0.1223/-0.1577
CLF angle offset (rad) = 3.789 +0.096/-0.151
r = 1.7252 +0.3298/-0.2182
SQZ angle offset (rad) = -1.0304 +-0.4
Note that most of the error bars have become larger to get to the point where RMSE increase by 10% as other parameters are free to move during each tweak.
Daniel also suggested another method to estimate uncertainties is to use covariance matrix. I have been having issue getting the function to spit out jacobian. This will take a little longer.
Here's another goodness of fit estimate using Chi^2, suggestion by Daniel:
Chi^2 = SUM( ((Y2-Y1 / dY))^2 ) ; Y2 is the fit, Y1 is measured data, dY is the uncertainty in the measured data.
I tweaked dY so that Chi^2 = number of data - number of parameter, this chi^2 should be the lowest.
Once I have dY, I tweaked each parameter and let other refit until I get Chi^2+1.
Below are each parameter with 1sigma uncertainty:
Loss (%) = 51.86 +3.84/-1.89
Phase noise (rad) = 0.1577 +0.0447/-0.0337
CLF angle offset (rad) = 3.789 +0.0235/-0.0399
r = 1.7252 +0.0913/-0.04
SQZ angle offset = -1.0304 +0.1142/-0.0674
The uncertainty has become much smaller with this method. Sadly the phase noise is still within 100mrad range even with the lower bound uncertainty.