L. Dartez, J. Kissel
This evening, we've started a collection of PCAL X lines in order to begin studying two things:
(1) Our O4 goal is to produce an estimate of the systematic error in the collection of calibrated data streams (be it CAL-DELTAL_EXTERNAL or GDS_CALIB_STRAIN or whatever intermediate product) in real time, or at least in low latency. To do so really means that we must be measuring it all the time. A transfer function between the PCAL drive, a "Delta L" itself, and whatever calibrated data product, also a "Delta L" should be unity in magnitude and zero in phase. If it's not, there's systematic error in that calibrated data product (or PCAL, but we'll set that aside for now). So, we've put in 5 new single-frequency excitations at amplitudes that made Louis and I happy, at roughly SNR 10 in a 128 [sec] FFT. We're considering different waveforms, see G2101248, but single lines are the standard typical "easy first guess" at "what's the best excitation waveform?"
Unfortunately, because the systematic error in the response function is most volatile in the 20-500 Hz region -- right where we're also most sensitive to gravitational waves -- that means we must sacrifice some sensitivity in order to get this real-time / low-latency estimate of the systematic error.
(2) BUT because we now have become quite comfortable with subtraction algorithms, and we have a very clean witness channel (the PCAL channel itself), we can subtract out this excitation. The real question is *how well* can we subtract out this excitation, and what are the non-linear implications / leftovers from the subtraction. So, simultaneously, we're also training our subtraction algorithms with this data, to ask "are we really going to be OK with subtracting this out?"
We intend to leave these on for a *while* to track how the systematic error evolves over time (a) within a long lock stretch, (b) at the beginning of a lock stretch where we've powered up quickly, (c) between lock stretches, (d) across Tuesdays, etc. We may be adjusting the amplitudes and frequencies along the way, as we gather data and learn more about what's needed, but the point is to get long days worth of time such that we learn lots, and the CW group has time to make statements about the impact.
Here're the line parameters that we'll leave in for at least a week that we picked today:
Line frequencies in [Hz]
H1:CAL-PCALX_PCALOSC4_OSC_FREQ 56.39
H1:CAL-PCALX_PCALOSC5_OSC_FREQ 77.73
H1:CAL-PCALX_PCALOSC6_OSC_FREQ 102.13
H1:CAL-PCALX_PCALOSC7_OSC_FREQ 283.91
H1:CAL-PCALX_PCALOSC8_OSC_FREQ 33.43
Line Amplitudes in [(meaningless) DAC ct]
H1:CAL-PCALX_PCALOSC4_OSC_SINGAIN 5
H1:CAL-PCALX_PCALOSC5_OSC_SINGAIN 10
H1:CAL-PCALX_PCALOSC6_OSC_SINGAIN 20
H1:CAL-PCALX_PCALOSC7_OSC_SINGAIN 200
H1:CAL-PCALX_PCALOSC8_OSC_SINGAIN 5
We also -- as a test of the range of the PCAL system -- turned back ON the "roaming line" that is the constant measurement of the sensing function between 1 kHz and 5 kHz, that moves around every ~24 hours of nominal low noise time. We've not resurrected the automation to make this actually sweep in frequency, but we've at least turned the line back on to test the range it takes up. We've found that the former amplitude 30k [DAC ct] was too much while *also* driving these new low-frequency "systematic error lines," so we backed off the roaming line's amplitude by half to 15k [DAC ct]. We'll suffer the uncertainty in *that* measurement, but the astrophysical demands for precision at those frequencies are much less stringent.
Attached is a quick / inaccurate measurement of the ASDs of both channels, and a look at the coherence with a 128 [sec] FFT. At the moment, the worst coherence is ~0.1 at 283 Hz, which, with 25 avgs corresponds to an uncertainty of sqrt( (1 - C) / (2NC)) = 0.42 = 42%. So, we already know, at this amplitude, we'll need to take longer FFTs.
These new settings have been saved into the SDF system.
The configuration described above was stable by 2022-07-29 23:50 UTC, so data analysis should begin there.
[Maddie W., Les W.]
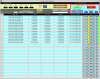
I have taken a first look at how these new lines will work to measure calibration systematic error. So far I have looked at:
- The coherence of pcal and strain at the oscillator frequencies over an hour of low-noise time
- The coherence uncertainty (sqrt((1-C)/(2NC))), where C is coherence and N is the number of averages (or medians in this case)
- The transfer function between pcal and strain at the oscillator frequencies (H1:GDS-CALIB_STRAIN / H1:CAL-PCALX_RX_PD_OUT_DQ)
I have experimented with different FFT lengths to figure out what could work with our current line heights. I looked at a 1-hour stretch of low-noise time (GPS times 1343181883-1343185483).
For each of the calculations in the table below, FFTs of the specified length were medianed over the hour-long lock stretch with a 50% overlap. Note: This means the number of medians is different for each choice of FFT length. The shorter FFT lengths had a larger N, which made the uncertainties fairly comparable across each choice of FFT length.
We are still working on making good visuals for this type of information, so I don't have any trend plots made right now (coming soon!).
FFT length: 64 s
| Frequency (Hz) | Coherence | Coh. Unc. | Transfer function magnitude | Transfer function phase (deg) |
|---|---|---|---|---|
| 56.39 |
0.977723 |
0.0100855 |
1.05 |
-0.77 |
| 77.73 |
0.989045 |
0.00703192 | 0.92 | -1.27 |
| 102.13 |
0.993892 |
0.00523788 | 0.88 | -7.05 |
| 283.91 |
0.997602 |
0.00327583 | 1.01 | -24.3 |
| 33.43 |
0.981174 |
0.00925512 | 1.10 | -6.87 |
FFT length: 128 s
| Frequency (Hz) | Coherence | Coh. Unc. | Transfer function magnitude | Transfer function phase (deg) |
|---|---|---|---|---|
| 56.39 |
0.988017 |
0.0104062 |
1.04 |
-1.01 |
| 77.73 |
0.994885 |
0.00677528 | 0.92 | -1.06 |
| 102.13 |
0.996820 |
0.00533699 | 0.87 | -6.74 |
| 283.91 |
0.998857 |
0.00319641 | 1.02 | -24.5 |
| 33.43 |
0.991915 |
0.00853088 | 1.11 | -6.42 |
FFT length: 256 s
| Frequency (Hz) | Coherence | Coh. Unc. | Transfer function magnitude | Transfer function phase (deg) |
|---|---|---|---|---|
| 56.39 |
0.994031 |
0.0107461 |
1.03 |
-0.39 |
| 77.73 |
0.997854 |
0.00643102 | 0.92 | -1.16 |
| 102.13 |
0.998022 |
0.00617364 | 0.87 | -6.75 |
| 283.91 |
0.999584 |
0.00282902 | 1.02 | -24.5 |
| 33.43 |
0.995208 |
0.00962276 | 1.11 | -6.65 |
FFT length: 512 s
| Frequency (Hz) | Coherence | Coh. Unc. | Transfer function magnitude | Transfer function phase (deg) |
|---|---|---|---|---|
| 56.39 |
0.995964 |
0.0120303 | 1.04 | 0.522 |
| 77.73 |
0.998930 |
0.00618508 | 0.92 | -0.90 |
| 102.13 |
0.998742 |
0.0067071 | 0.87 | -6.95 |
| 283.91 |
0.999755 |
0.0029584 | 1.02 | -24.7 |
| 33.43 |
0.997104 |
0.0101847 | 1.11 | -7.19 |