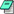First observed as a persistent mis-calibration in systematic error monitoring Pcal lines which measure PCAL / GDS-CALIB_STRAIN affecting both LLO and LHO, [LLO Link] [LHO Link], characterised by these measurements consistently disagreeing with the uncertainty envelope.
It us presently understood that this arises from bugs in the code producing the GDS FIR filters there exists a sizeable discrepancy, which Joseph Betzwieser is spear-heading a thorough investigation to correct,
I make a direct measurement of this systematic error by dividing CAL-DARM_ERR_DBL_DQ / GDS-CALIB_STRAIN , where the numerator is further corrected for kappa values of the sensing, cavity pole, and the 3 actuation stages (GDS does the same corrections internally). This gives a transfer function of the difference induced from errors in the GDS filters.
Attached in this aLog, and its sibling aLog in LLO, is this measurement in blue, the PCAL / GDS-CALIB_STRAIN measurement in orange, and the smoothed uncertainty correction vector in red. Attached also is a text file of this uncertainty correction for application in pyDARM to produce the final uncertainty, in the format of [Frequency, Real, Imaginary].
After applying this error TF, the uncertainty budget seems to agree with monitoring results (attached).
After running the command documented in alog 70666, I've plotted the monitoring results on top of the manually corrected uncertainty estimate (see attached). They agree quite well.
The command is:
python ~cal/src/CalMonitor/bin/calunc_consistency_monitor --scald-config ~cal/src/CalMonitor/config/scald_config.yml --cal-consistency-config ~cal/src/CalMonitor/config/calunc_consistency_configs_H1.ini --start-time 1374612632 --end-time 1374616232 --uncertainty-file /home/ling.sun/public_html/calibration_uncertainty_H1_1374612632.txt --output-dir /home/ling.sun/public_html/
The uncertainty is estimated at 1374612632 (span 2 min around this time). The monitoring data are collected from 1374612632 to 1374616232 (span an hour).
J. Kissel, J. Betzwieser
FYI: The time at which Vlad used to gather TDCFs to update the *modeled* response function at the reference time (R, in the numerator of the plots) is
2023-07-27 05:03:20 UTC
2023-07-26 22:03:20 PDT
GPS 1374469418
This is a time when the IFO was well thermalized.
The values used for the TDCFs at this time were
\kappa_C = 0.97764456
f_CC = 444.32712 Hz
\kappa_U = 1.0043616
\kappa_P = 0.9995768
\kappa_T = 1.0401824
The *measured* response function (GDS/DARM_ERR, the denominator in the plots) is from data with the same start time, 2023-07-27 05:03:20 UTC, over a duration of 384 seconds (8 averages of 48 second FFTs).
Note these TDCF values list above are the CAL-CS computed TDCFs, not the GDS computed TDCFs. They're the value exactly at 2023-07-27 05:03:20 UTC, with no attempt to average further over the duration of the *measurement*. See attached .pdf which shows the previous 5 minutes and the next 20 minutes. From this you can see that GDS was computing essentially the same thing as CALCS -- except for \kappa_U, which we know
- is bad during that time (LHO:72812), and
- unimpactful w.r.t. the overall calibration.
So the fact that
:: the GDS calculation is frozen and
:: the CALCS calculation is noisy, but is quite close to the frozen GDS value is coincidental, even though
:: the ~25 minute mean of the CALCS is actually around ~0.98 rather than the instantaneous value of 1.019
is inconsequential to Vlad's conclusions.
I'm adding the modeled correction due to the missing 3.2 kHz pole here as a text file. I plotted a comparison showing Vlad's fit (green), the modeled correction evaluated on the same frequency vector as Vlad (orange), and the modeled correction evaluated using a dense frequency spacing (blue), see eta_3p2khz_correction.png. The denser frequency spacing recovers error of about 2% between 400 Hz and 600 Hz. Otherwise, the coarsely evaluated modeled correction seems to do quite well.
The above error was fixed in the model at GPS time 1375488918 (Tue Aug 08 00:15:00 UTC 2023) (see LHO:72135)