On Wednesday, while testing filters in the "New DARM" state, the ETMX roll mode was inadvertently rung up (I assume it was ETMX because that was the suspension we were changing filters on). It dominated the DARM RMS long enough that I figured I could get a fit of the ringdown and measure the via the OMC DCPD sum.

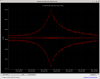
I extracted the data during the ringdown time, after the filter that was driving the mode was turned off. I split the data up into smaller segments and estimated the height of the peak in the ASD and fit a decaying exponential. The estimated Q of this mode is about 6173 with an estimated frequency of 13.759 Hz. The resulting plot of the exponential fit is show in the third attachment. I performed the fit by taking the logarithm of the data and fitting a linear regression- the resulting r-squared value was 0.998, so I think this is a very good fit. However, I made no estimate of the background for this fit, so there may be some bias in the fit itself. I tried to perform a more precise fit of the damped sinusoid using a digital heterodyne, but I'm unhappy with my curve fitting algorithm. I think ultimately that may be a better way to get a more accurate Q (but if I'm being honest I am unlikely to follow through on that work unless someone really wants me to).

However, I think this is still a pretty good measurement, especially given that Jeff measured a Q of about 7000 for the ETMY roll mode. It is a bit high, given the goal of the BRD was "a Q between one and a few thousand" (quoting Norna's slides from https://dcc.ligo.org/LIGO-G1600371). From a practical point of view, within 10 minutes the roll mode was back to nominal anyway.