I have compiled the results of in-air measurements during installation and in-vacuum measurements from the alogs; 14231 LLO (including corrections mentioned in alogs 21652 and 27901) and 17610 at LHO (including corrections mentioned on the comments).
In the case when a frequency split is shown on in-vacuum measurements we have taken the average of both frequencies. I have grouped these numbers per front and back fibres, then per test mass and then per detector, finally I obtained the difference as (in-vacuum – in-air) including the sign:
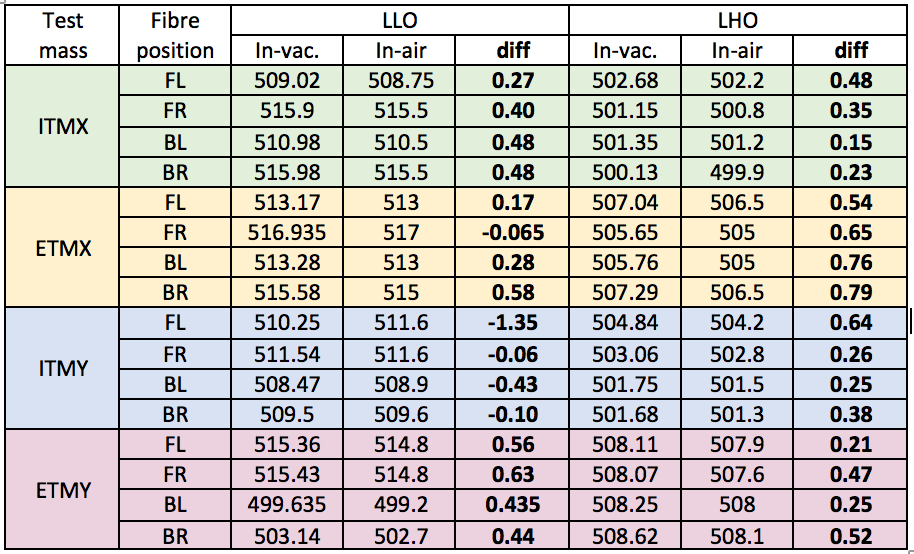
We notice that in most cases the frequency difference is always positive, so frequency increases when moving the suspension to in-vacuum.
The increase in frequency is always a few hundred mHz (mean of 0.3Hz and median of 0.4Hz), with a clear outlier on LLO_ITMY_FL (which as explained here seems to be involved with uncertainty in the identification).
There is not clear difference in frequency variation between front and back fibres (especially no sign difference) which would indicate pitch effect.
However, notice that as per the Technical document T1700399 the expected increase in frequency due to buoyancy is of 0.14Hz, and the variation in frequency due to pitch angles of 2mHz is of 0.33Hz (although that would be an opposite sign change between front and back fibres). Therefore while the observed changes cannot be explained through pitch and buoyancy alone, they are of the same order.
Further discussions on the results presented here has led to realize that the in-air measurements of the violin modes fundamental frequencies have a potential error of about 0.25Hz (as an example here are measurement results for LHO ITMX suspension). In base of this and to better understand the actual differences between in-air and in-vacuum measurements, now that we have very accurate measurements in-vacuum, it would be informative to measure in-air values once the suspensions are taken out.
The in-air measurements have so far been done by acoustically driving the violin mode resonances. During this measurements the frequency of the driving acoustic signal is changed as a sweep sine. Because the in-air Q of the violin modes is considerably less than the in-vacuum values of 1 billion, if the sweep sine drive is not done with suitable slow pace then the observed a violin mode excitation at a frequency on the sweep sine which actually correspond to a previous frequency of the sweep but took some time to ring up. Under this assumption, if the sweep sines were driven down (from high frequencies to lower frequencies) then there would be a consistent error on the measured in-air frequencies with values being lower than in-vacuum ones.
A way to improve the acoustic excitation could be by building a tower of speakers so that they could inject more energy into the violin modes of the fibres. Also be sure to drive the sweep sine at enough low pace or inject random noise excitation instead. Finally a lot of information could be gained by in-air measurements of higher order harmonics, this would help on characterization and understanding of higher order inharmonicity as well as higher order mode identification.
In order to proceed with the in-air measurements of the violin mode and its harmonics during the installation of the suspensions in the near future (as well as measuring the already install suspensions once removed), we have built in Glasgow a line array of 24 speakers of 60 cm length to match the length of the fused silica fibres. Its lightweight and compact design make it suitable to locate it parallel and in close proximity to the fibre that wants to be excited.
This line array produces considerable sound from 300Hz and well above several kHz making it suitable to excite the fundamental mode and up to the 6th harmonic and beyond.
A more complete description can be found on the technical document T1700414T1700414.
It is relevant to this alog to remember that while preliminary FEA modelling of the actual fibre profiles measured during installation of the LHO ITMX suspension (end of March 2014), has been used to predict in general terms the observed departure of the frequencies of the violin mode harmonics from whole multiples of the fundamental (“inharmonicity”):
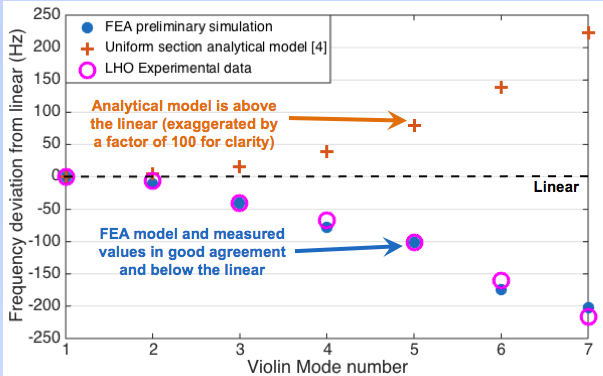
However this preliminary results show that this prediction is not yet accurate to the few Hz level required for identification:
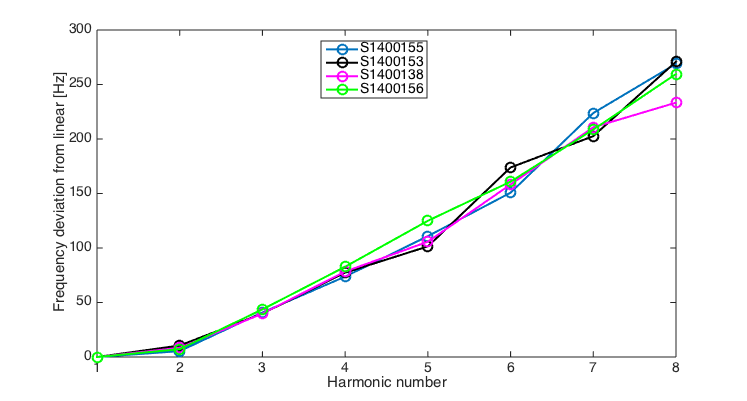
In order to complete the list of possible causes for the different inair and invacuum measured violin mode frequencies, I add next the contributions suggested recently by Norna, Dennis and Jon Feicht:
Violin modes frequency variations due to air damping
Air damping lowers the in-air measured violin mode frequency by a value inverse proportional to the violin mode’s Q-factor. Such that the maximum frequency for a damped oscillator (fm) is related to the undamped maximum frequency (f0) by:
fm = f0 ∙ sqrt[1-1/(2∙Q2)]
A quick look at recent in-air measurement on the LHO alog 38743 suggest a Q of at least 100 in-air at the ~ 500 Hz fundamental mode. This would give a in-air measured frequency value of the fundamental of 0.012Hz lower than in-vacuum.
Violin modes frequency variations due to mass/length of the fibre decreasing as the water desorbs from the silica fibre in vacuum
The mass loading on the fibre, due to water adsorption in-air, should in principle cause the in-air measurement of the violin mode fundamental frequency to be lower than in-vacuum, as once much of the water is pumped off the fibre in vacuum the frequency should increase. Dennis Coyne calculated that about ~3500 monolayers of water (each 2.5 angstroms thick) would be necessary to cause a 1 Hz shift at 500 Hz, due to mass loading alone. It is commonly asserted in vacuum literature that stainless-steel surfaces of a vacuum system exposed to air can start with "hundreds of monolayers of water".
However fused silica is hydrophilic and the interaction of silica surfaces and water is complex; Surfaces of silica under water can swell and form layers of silica gel1. The modification of the fused silica surface by the chemisorption and physisorption of water may even lead to a reduction in the elastic modulus of the fused silica in the outer layers.
References
[1] V.V. Yaminsky, et. al., "Interaction between Surfaces of Fused Silica in Water", Langmuir 1998, 14, 3223-3235.





