Dan, Kiwamu, Evan
Summary
Tonight we worked on getting the interferometer back to its low-noise state. We are stable at 10 W, but there is some instability at higher powers.
Details
ITM steering
First, at 3 W we manually steered the ITMs to a good recycling gain (38 W/W), and then updated the TMS QPD offsets. We also locked the arms in green, adjusted the green QPD offsets for maximum buildup, and then updated the ITM camera references. Then we re-enabled the ITM loops in the guardian. This allowed us to power up all the way to 21 W without significant degredation of the recycling gain.
After that, we were able to consistently engage the ASC with the guardian.
Power-up issues
However, we found that at 21 W the interferomter suddenly unlocks in a matter of minutes. There seems to be no instability in the arm or sideband buildups before the lockloss. We looked at OMC DCPD signals for signs of PI, but we did not see anything ringing up during any of our short high-power locks. Some times to look at are 02:29:50, 02:59:50, 04:57:30, 06:55:00, all 2015-05-26 UTC. But any of the other 21 W locklosses in the past 12 hours follow this pattern.
We measured the OLTFs of PRCL, MICH, SRCL, and DARM before and after powering up, but they all look fine and did not change with power. For CARM, we start at 3 W with a UGF of 14 kHz with 47° of phase. Then during power-up, the electronic gain is automatically adjusted to compensate for the increased optical gain. The algorithm for this was shooting a little high, so after power-up the UGF was more like 27 kHz with 30° of phase. This is probably fine, but we adjusted the algorithm anyway, so that the UGF is placed at 19 kHz, with 45° of phase. Anyway, this did not solve the lockloss issue.
We also tried locking at some lower powers. At 15 W the interferometer lasted for about 15 minutes before unlocking. At 10 W, the lock time seems to be indefinite (at least 90 minutes).
DARM crossover
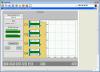
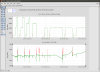
Using FM9 in ETMY L1 LOCK L (zero at 2 Hz, pole at 5 Hz), we were able to push the L1 crossover from <1 Hz to 1.7 Hz by adjusting the filter gain from 0.16 to 0.31. Measurement attached, showing before and after. This is not included in the guardian. By pushing up the crossover, the rms drive to L2 decreases from >10000 ct to about 6000 ct or so.
Other
For the record, we did not notice any kicks to the yaw of IMC REFL tonight.