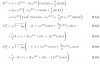craig.cahillane@LIGO.ORG - posted 15:19, Friday 09 September 2022 - last comment - 13:25, Monday 12 September 2022(64928)
Absolute DARM calibration from September 1, 2022
We have been investigating the loss in our output path, especially the discrepancy between DCPDs and AS_C. To facilitate this in part, I measured the DARM sensing plant on September 1 to see what our optical gain was versus what we might expect from the given power on the beamsplitter.DARM sensing measurement -------------------I did the usual calibration team swept sines for the DARM loop suppression and PcalY injections, then used a modified pydarm example code to process this measurement. This processing includes application of two poles to calibrate the PCAL into meters, some accounting for some AA filters which mostly affect phase at these frequencies, light travel delay, and a correction factor for the simple pole approximation vs infinite pole response. I also measured and calibrated the numerator from DARM IN1 cts to OMC DCPD mA. This script is in/ligo/home/craig.cahillane/Git/darmplant/code/example_process_optical_response.pyThe result is shown in the first plot. Below 15 Hz the measurement breaks down and does not follow any expected model, likely due to cross-coupling from other loops. This data was discarded for the MCMC.BnC MCMC --------I ran an 4-parameter MCMC on this data to fit a "lossy BnC model" to it. The four parameters were1. SRC detuning 2. power on the beamsplitter 3. loss in the SRC 4. loss in the output pathFixed parameters for the lossy BnC model were1. homodyne angle = 90 degs 2. arm loss = 60 ppm 3. local oscillator power = 23.8 mW 4. arm_length = 3994.5 m 5. src_length = 56.01 m 6. itm_trans = 0.015 7. etm_trans = 4e-6 8. srm_trans = 0.3234Arm loss was found to have a very small effect on the DARM plant unless the numbers were unrealistically large (~1000 ppm). For this reason I fixed it at 60 ppm. Similar reasoning behind the homodyne angle fix at 90 degrees. The power on the beamsplitter was initialized asPbs = Pin * PRG, withPin = 48 W, PRG = 52.8, yieldingPbs = 2.534 kW. The prior on the power on the beamsplitter was a gaussian with 5% standard deviation. The other parameters have flat priors. The MAP parameters are shown in the second plot. The corner plot is shown in the third. The MAP parameters found were1. SRC detuning = 89.92 +- 0.01 degs 2. power on the beamsplitter = 2.482 +- 0.13 kW 3. loss in the SRC = 0.92 +- 0.07 % 4. loss in the output path = 35.234 +- 3.6 %Discussion ----------This loss in the output path is very high, consistent with the discrepancy from alog 64240. The 5% prior on the power on the beamsplitter dominates the posterior results. The loss in the output path is largely covariant with the power on the beamsplitter, so this prior may be determining two parameters' posteriors. SRC detuning is largely determined by the low frequency magnitude uptick which may or may not be due to an actual DARM optical spring (could be from cross-coupling). But it is unlikely to be much different than 90 degrees. The best-determined parameter is the loss in the SRC, which depends mostly on the DARM pole frequency. We've run into a bit of a chicken-and-egg problem with the power on the beamsplitter and the output path losses. Thanks to the HAM1 vent results alog 63510, we trust our input power incident on the PRM to 3% or so. I also verified the PRG calculation a couple of times via the usual method of arm transmission comparison between single arm lock and full lock. However, we know from the squeezers that 35% loss in the output path is impossible based on the observed squeezing in full lock (see Vicki's wiki). A more realistic number is more like 20%, according to them. So, the mystery still abounds. We know our OMC alignment and mode matching may not be perfect. We should double check out DCPD calibration into mA as well.alogs: ------Discrepancy in carrier power between OMC DCPDs and AS_C: alog 64240 Check of OMC finesse using April 2022 single-bounce OMC scan: alog 64582 DARM offset reduction test on September 1 2022: alog 64818 Keita's AS_C calibration via integrating sphere: alog 62213 HAM1 vent input power budget 2022: alog 63510 H1 Squeeze loss budget (Vicki's wiki)code ----Code is in thedarmplantgit repo: https://git.ligo.org/darmplant/darmplant MCMC code is incode/mcmc/darm_plant_lossy_bnc.pyEDIT: -----Daniel clarifies for us that this result of 35% output path loss indicates a 20% reduction of optical gain when compared to a lossless output path. The "lossy BnC" DARM plant model I fit iswhere the DARM optical gain goes like sqrt(1 - λpd) where λpd is the output path loss. AS_C reports 40% higher optical gain than OMC DCPD SUM in alog 64240. So with either PD, we are missing by 20% according to this fit.
Images attached to this report
Non-image files attached to this report
Comments related to this report
One possible explanation for this loss of optical gain could be a rather large mode mismatche and/or misalignment of the OMC. Since the squeezer mode matching and alignment is somewhat independent, it is imaginable that the apparent losses in the squeezer path are lower than in the GW signal path. There is also about 4x more carrier light in front of the OMC than in transmission presuambly due to a large contribution from higher-order modes. The field generated by these carrier HOMs could serve as an additional local oscillator for the mismatched GW signal, and hence elevate the optical gain as measured before the OMC above what you would expect from the DCPD power alone.
A brief note on the DARM pole and SRC loss.
In the past I've reported this strong dependence of the DARM pole on SRC loss.
The way I've found the DARM pole in alog 58658 may introduce a systematic bias from the usual single pole approximation.
Recently, this came under scrutiny as Lee McCuller's paper reports smaller SRC losses in Table 1 of https://arxiv.org/abs/2105.12052 than I do for O3.
First, I mention that for BnC SRC losses are strictly scattering losses: "We [BnC] describe the loss inside the SR cavity by the fraction of photons lost at each bounce of the interior field off the SR mirror"
So no mode mismatch loss is rigorously considered by the "lossy BnC" model used above.
However, mode matching loss may be grossly incorporated in some way by the SRC loss parameter which we cannot here distinguish from scattering loss.
The way I find the DARM pole in alog 58658 was by finding the where the denominator M_L of the BnC lossy model (Eq. 5.7 from https://arxiv.org/abs/gr-qc/0102012) above equals zero.
Plot 3 shows the magnitude and phase of M_L, and the DARM pole corresponds to the dip between 400-500 Hz.
When I do this for the model fit to the measurement above, I find a DARM pole = 455.7 Hz.
However, if I simply cut off the data at 30 Hz and fit a simple pole + gain model H(f)= gain / (1 + I ff/ pole),
I find the DARM pole = 452.6 Hz (See Plot 1).
This is a 3 Hz difference.
To ensure I was comparing apples to apples, I also fit the simple pole + gain model to the full BnC model (also cut off at 30 Hz). See plot 2.
This yielded 452.0 Hz.
So it appears that numerically finding the zero in the denominator overestimates the DARM pole by around 3 Hz compared to the usual single pole approximation.
Non-image files attached to this comment
Tagging CAL.