Naoki, Camilla, Sheila
We had another look at some signals that we could use to track or servo the SQZ angle.
We turned the ADF back on, making a line at 1.3kHz in DARM, and tuned the demod phase for the ADF so that the SQZ angle readout was 0 for the angle we've been using for observing in this lock. Camilla added a bandstop at 1.3kHz in the SQZ BLRMS4, sum and null channels and checked that the ADF isn't dominating those. We did a sweep of the CLF6 demod phase like this, with the dither amplitude reduced comapred to Wed (0.01 instead of 0.03 CLK gain).
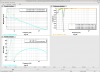
In the first attachment we are using BLRMS 4 to demodulate for the noise lock signal, the second cursor shows that the zero crossing of the ADF SQZ angle and the noise lock both correspond roughly with the minimum of noise in the BLRM4 (1kHz BLRMs). This isn't the same phase as the one that minimizes the brown trace, a blrms centered at 350 Hz. This means we have a frequency dependence of the SQZ angle, so we should probably look into things like the SRCL offset that might be causing this.
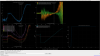
Naoki then turned the ADF phase with the SQZ angle set to minize BLRMS3, as shown in the second screenshot from Camilla (at the begining here you can see that Naoki set the ADF phase so SQZ ANG was zero for CLF demod phase of 145). We repeated the sweep and see that we have lower SNR for the noise lock using this lower frequency BLRMS, and that the ADF as it is now wouldn't make a good error signal for this sqz angle because it doesn't really go negative.
Detchar: We are planning to leave the ADF on over the weekend, which will create a line at 1.3kHz. We are hoping to use this to track changes in the squeezing angle over time.