J. Kissel
This week, I tried to pick up where I left off in modeling the DARM response of the IFO thermalization. I made some progress, but it's no where near "done," and I can't even yet say if this will be as promising as hoped. The purpose of this aLOG is to
(a) catch folks up to speed on this, since no one's really done anything since I left this in June 2023,
(b) share where I leave off such that someone else can pick it up, if need be, while I'm out on bonding leave.
(a) Catch up
Recall, where I'd left off in June 2023 was "disappointed and confused that -- for the 75W IFO -- the measured *sensing* function, C,
- did not evolve in a simple exponential way, with a single time constant, nor
- was it repeatable when looking at ~10 comparable thermalization periods (listed in LHO:69796).
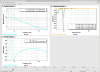
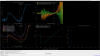
That disappointment, and how the sensing function evolved, was best conveyed with 3D bode plots where I showed the magnitude and phase as a function of frequency and time, or frequency and arm cavity power level (LHO:69898).
Regardless of the disappointment, I binned the sensing function transfer function answers in to arm power levels from the ~10 data thermalizing stretches, and fit those binned collections of transfer functions at each arm power to a GPR (LHO:70150)."
Thereafter, because we were disappointed and confused,
- We never used the GPR fits in the *model* of the *response function* systematic error over which the data analysis teams marginalize there astrophysical parameter estimation uncertainty,
- We never made the same analysis of the measured *sensing* function for the 60W data, even though we *eventually* gathered a comparable amount of data with the "thermalization" lines on between June 2023 and Aug 2023 (LHO:72950), and
- We concocted a "shot in the dark" idea to look at the measured *systematic error function,* eta_R = dL PCAL [m] / dL GDS, as a function of thermalization, because (theoretically) the sensing function "does not substantially contribute" to the response function below ~30 Hz where the sensing function is rapidly evolving during thermalization.
Remember, from T1900169, the measured *systematic error function,*
eta_R = dL_PCAL [m] / dL_GDS [m]
is equivalent to
= (true response function R=(1+G)/C measured by PCAL) / (modeled response function R=(1+G)/C produced by the calibration pipeline)
= which can be derived from the live transfer function (H1:CAL-PCAL[X/Y]_RX_PD_OUT_DQ) / (H1:GDS-CALIB_STRAIN)
assuming that
- at certain frequencies, we have constant, loud, PCAL injections *on* actively displacing the test masses, causing DARM (i.e. dL) displacement well above the detector's noise floor, and
- one "just" applies the "PCAL corrections" to convert the channels H1:CAL-PCAL[X/Y]_RX_PD_OUT_DQ into dL_PCAL [m], and multiplies H1:GDS-CALIB_STRAIN by, L to get dL_GDS [m].
The problem with using this measured *systematic error function* eta_R, rather than the directly measured *sensing function,* is that the constituent channel GDS-CALIB_STRAIN can have lots of other systematic error in it, besides the effects of thermalization which can and will -- at best -- confuse, -- at worst, invalidate -- any model of the thermalization you derive from it.
From Aug 2023 to Oct 2023, we slowly came to understand all the *other* systematic error that was in play during these times where we had extra PCAL lines ON to measure the thermalization. This effort culminated in the "Record of Real-Time Calibration Pipeline Parameter Changes: O4 (and ER15) -- H1" (T2300297), which helped us realize that there were two other systematic errors that significantly impacted H1:GDS-CALIB_STRAIN during these times:
(1) The identification that we had accidentally excluded a 3.2 kHz pole from our model of the ETMX TST Stage actuator [[impactful at all times in O4 until it was fixed on Aug 07 2023]], and
(2) The identification that a poorly designed MICH-to-DARM feed-forward filter spoiled the GDS production of time-dependent correction factors [[impactful between Jul 20 2023 to Aug 08 2023]].
Both of these effects are modeled and explained extensively in LHO:72622 and all subsequent comments. But in short -- the message is that we now have a *model* of these systematic errors, so we can *remove* them from measured *systematic error function*, which hopefully leaves *only* the thermalization effects.
(b) Where I leave off
So, this is where I started this week (Nov 13 thru 17) -- with trying to execute as much of following plans as I could:
(i) Download all the necessary data to create the raw, measured *systematic error* transfer function during the ~22, 4 hour data stretches at 75 W (from LHO:69796), and 60 W (from LHO:72950), and save it to much lighter weight text files. Also record all the other same metrics that will eventually be needed to correct for systematic error (i.e. both CALCS and GDS TDCFs), and bin the answers as a function of arm cavity power to make 3D bode plots and GPR fits.
DONE Script to do this: download_and_save_respfunc_at_callines.py (at git hash 070f694b)
The data is saved to
/ligo/svncommon/CalSVN/aligocalibration/trunk/Runs/O4/H1/Measurements/SystematicErrorTFs/Thermalization/
75W/
60W/
with file names like
etaR_PCALdLmeas_over_GDSdLmodel_$pwr_$gpsstart-$gpsstop_mag*.txt # 120 times rows of abs(PCAL dL [m] / GDS dL [m]) at 14 freq points
etaR_PCALdLmeas_over_GDSdLmodel_$pwr_$gpsstart-$gpsstop_pha*.txt # phase (in radians) of (PCAL dL [m] / GDS dL [m])
etaR_PCALdLmeas_over_GDSdLmodel_$pwr_$gpsstart-$gpsstop_unc*.txt # coherence-based uncertainty of PCAL dL [m] / GDS dL [m]
etaR_PCALdLmeas_over_GDSdLmodel_$pwr_$gpsstart-$gpsstop_tdcfs_ccs.txt # CAL-CS TDCFs at each time step
etaR_PCALdLmeas_over_GDSdLmodel_$pwr_$gpsstart-$gpsstop_tdcfs_gds.txt # GDS TDCFs at each time step
etaR_PCALdLmeas_over_GDSdLmodel_$pwr_$gpsstart-$gpsstop_timetime*.txt # mesh grid of 120 times vs 14 frequency points
etaR_PCALdLmeas_over_GDSdLmodel_$pwr_$gpsstart-$gpsstop_pwrpwr*.txt # meas grid of 120 power levels vs. 14 frequency points
where $gpsstart and $gpsstop are the start and stop of each segment.
(ii) Figure out what pyDARM parameter sets are valid and representative for the 75W and 60W detectors, load in those light-weight text files of the raw, measured *systematic error* transfer function in a script that uses those pyDARM parameter sets, the pyDARM model, and TDCFs at the time to correct for the (1) and (2) known systematic errors, and saves both the modeled correction and updated eta_R the transfer function, that is (supposedly) containing only "thermalization" systematic error.
DONE Script to do this: remove_othersyserr_from_respfunc_at_callines.py (at git hash 557399c7)
The data is saved to
/ligo/svncommon/CalSVN/aligocalibration/trunk/Runs/O4/H1/Measurements/SystematicErrorTFs/Thermalization/
75W/
60W/
with file names like
etaR_thermonly_PCALdLmeas_over_GDSdLmodel_$pwr_$gpsstart-$gpsstop_mag.txt # abs(PCAL dL [m] / GDS dL [m]) after removing (1) and (2)
etaR_thermonly_PCALdLmeas_over_GDSdLmodel_$pwr_$gpsstart-$gpsstop_pha.txt # phase (in radians) of (PCAL dL [m] / GDS dL [m]) after removing (1) and (2)
GDSdL_corr_$pwr_$gpsstart-$gpsstop_mag.txt # modeled abs(R_good / R_bad) systematic error correction that was removed
GDSdL_corr_$pwr_$gpsstart-$gpsstop_pha.txt # modeled phase(R modeled good) in radians
Notes:
- I've (perhaps incorrectly) assumed that there is *no* update to the uncertainty of the measured transfer function. I think this is valid for the model of the missing 3.2 kHz pole, but I would question the validity of this during the application of the correction for bad TDCFs. But I here (again, boldly) assume it's OK, because "GDS TDCFs have the same uncertainty as CALCS TDCFs." If I had more time, I would grab the TDCF uncertainty as well, and use it to correctly augment the _unc*.txt files, but I did not.
- While I saved, additionally, separately, the eta_R answers from PCALX (with 9 frequency points) and PCALY (with 5 frequency points), from the combined answers (with 14 frequency points), I did *not* create more files
(iii) Make a ton of plots showing the results of (i) and (ii), be they 3D bode plots, or regular bode plots. The challenge here is that, for the 60 W data between Jul 20 2023 to Aug 08 2023, the *known* systematic error (2) is a *strong* function of thermalization and TDCFs, so each 2-minute stride is going to have a slowly evolving correction to dL GDS [m], so deciding how to plot that will be ... "fun."
But, in the end, the goal is to have enough understanding and intuition of the data that you can make the right choices about binning and GPR fitting.
OR, (I doubt it, but) you may find that "the response function systematic error that results from the sensing function going bonkers below 30 Hz during thermalization is negligible compared to the current levels of uncertainty in the *modeled* systematic error, so we're not going to do anything."
NOT DONE Try to model the script to do this after compare3d_sensing_darm_comb.py using LHO:69898 (the comment!) as your guide.
(iv) Bin the data into arm power levels, and fit to GPR. You'll hopefully have 2 sets of results, one for 75W data and one for 60W data.
NOT DONE Try to model the script to do this after gpr_sensing_darm_comb_pwrslices.py, using LHO:70150 as your guide.
(v) Figure out *all* times when thermalization apply the GPR fits, and correct the *modeled* systematic error function over which data analysis groups use to marginalize their astrophysical parameter estimation.
NOT DONE Talk to Lilli, Louis, Ethan, and the rest of the calibration team about how to best do this.
Happy hunting, y'all -- see you in Feb 2024!